textlize pricing account
Why Deep Learning Works Unreasonably Well
Cover

00:34:08

深度学习为何效果惊人？几何视角揭示神经网络的强大奥秘

核心发现：

  • 万能近似定理证明两层神经网络理论上可拟合任意函数
  • 实际训练中浅层网络需要指数级神经元解决复杂问题
  • 深层网络通过分层折叠实现指数级区域划分能力
  • ReLU激活函数创造非线性折叠几何结构
  • 梯度下降训练存在局部最优陷阱

万能近似定理的几何诠释

1989年George Cybenko提出的万能近似定理证明：对于比利时与荷兰边境的复杂地理边界，存在一个双层神经网络可以任意精度拟合该边界。从几何视角看，神经网络通过分层空间变换实现这一能力：

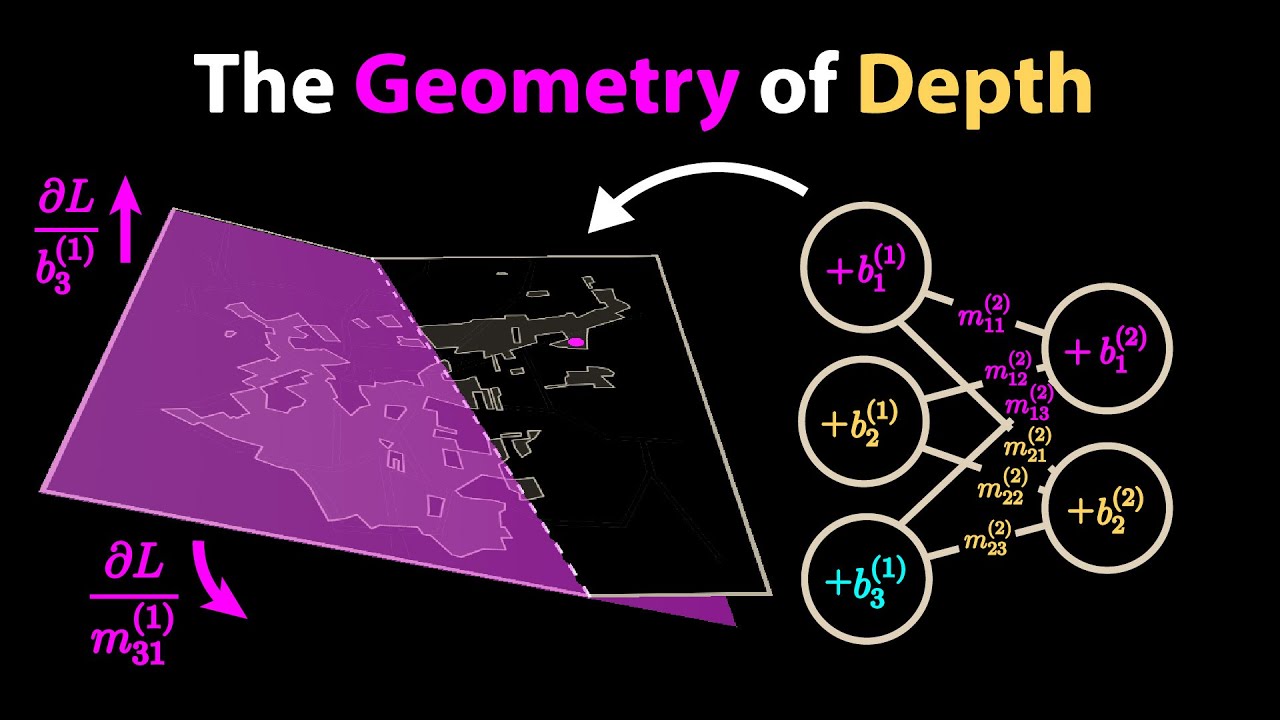
🔹 第一层操作（空间折叠）

每个神经元通过ReLU激活函数沿特定折线折叠输入空间（如地图），权重控制折线位置。当输入值小于零时，ReLU将其输出设为零，形成"折叠"效果。

🔹 第二层操作（曲面重构）

神经元对折叠后的平面进行缩放和组合：权重决定弯曲方向和幅度，负权重实现区域翻转。多个折叠平面相加形成分片线性曲面，折线将地图划分为多个区域。

浅层网络的实践困境

尽管定理保证双层网络的理论可行性，实际训练中却面临严峻挑战。使用100,000个神经元的浅层网络训练比利时边境问题时：

神经元数量 拟合效果 关键限制
100,000 仍存在边界误差 梯度消失/爆炸
10,000 基本轮廓但细节缺失 局部最优陷阱
128（单层） 粗糙近似 区域划分能力不足

根本问题在于：

  • 训练算法局限：梯度下降无法保证找到全局最优解，随机初始化可能导致模型陷入无效配置
  • ReLU的梯度截断：负值区域梯度为零，导致参数更新停滞
  • 理论需求与实践差距：某些函数类需要指数级神经元，100,000神经元可能仍不足

深度网络的指数级威力

将128个神经元重组为4层结构（每层32神经元）后，模型性能发生质变：

▍ 分层折叠机制

每层输出作为下一层输入，形成递归操作：
1. 第一层：基础线性折叠（2个神经元→4区域）
2. 第二层：复合曲面折叠（2神经元→10区域）
3. 深层：几何复杂度指数增长

▍ 区域划分理论

区域数量随层数指数增长：
• 2层网络：最大区域数多项式增长
• 4层网络：理论最大区域数达70,000,000+
实际32神经元5层网络即可精确拟合复杂边境

⚡ 关键突破：

深层架构中，单个神经元可创建多角度折线（如图中第二层神经元生成10个独特折点），这是浅层网络无法实现的几何表达能力。

训练过程的动态可视化

通过梯度下降训练5层网络的过程揭示：

  • 初始阶段（<100步）：快速捕获核心边界结构
  • 优化阶段：通过微观区域创建逐步细化边界细节
  • 死亡神经元现象：部分神经元输出恒为零，反映梯度下降的资源分配缺陷

深度学习的本质突破

▍ 理论启示

万能近似定理仅保证解的存在性，而深度架构通过：
• 指数级区域划分能力
• 参数效率提升
• 梯度传播优化
使实际训练可行

▍ 实践意义

几何视角解释了为何深度网络能：
• 用少量神经元解决复杂问题
• 学习高度非线性模式
• 突破浅层网络的计算瓶颈

神经网络通过分层空间折叠将简单线性变换转化为复杂决策边界，这种"几何复合"效应是深度学习超常表现的底层机制。尽管训练算法仍有局限，分层结构提供的指数级表达能力使其成为解决复杂模式识别问题的首选架构。

© 2025 textlize.com. all rights reserved. terms of services privacy policy